This post was contributed by Professor Sarah Hart of Birkbeck’s Department of Economics, Mathematics and Statistics and Head of the Pure Mathematics Research Group. Here, Professor Hart offers an insight into a major area of her research: sum-free sets
The set S = {1, 3, 5} is “sum-free”: if you add two numbers in S, the answer is outside S. So 1 + 3 = 4, and 4 is not in S.
There are many questions we could ask about sum-free sets. How big can they get? Are there infinite sum-free sets? The answer is yes – the set of all odd numbers is sum-free because the sum of any two odd numbers is even, and so lies outside the set. In fact this is also locally maximal (we cannot add any further elements to it while keeping it sum-free), because any even integer (see glossary below) is the sum of two odd integers so we cannot add any even integers to the set.
Having found this large sum-free set we might ask if we can divide up (partition) the set of integers into a small collection of sum-free sets. (Actually, the fact that 0 + 0 = 0 means we only look at the set of nonzero integers.) It turns out there is no way to partition the set of nonzero integers into a finite collection of sum-free sets, although there are partitions into an infinite number of sum-free sets.
Groups
The interesting thing about this set-up is that it can be generalised. The set of integers is just one example of a “group”, which is a set along with an operation which can combine two elements a, b of the set to produce a third element a*b.
For the integers, the operation is addition: two integers added together produce another integer, so a * b is defined as a + b. There are three rules that the operation must satisfy. One is “associativity”, which for the integers translates as the property that for any integers a, b and c, we have (a + b) + c = a + (b+c).
There are countless examples of groups, for example the set of symmetries of any shape. The operation is composition – so the combination of a rotation integer (see glossary below) and a reflection is the symmetry obtained by doing the rotation followed by the reflection. Unlike the group of integers, many groups are finite.
The notion of a sum-free set
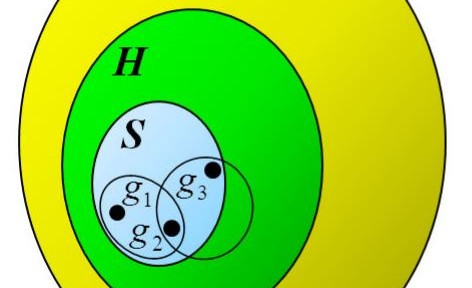
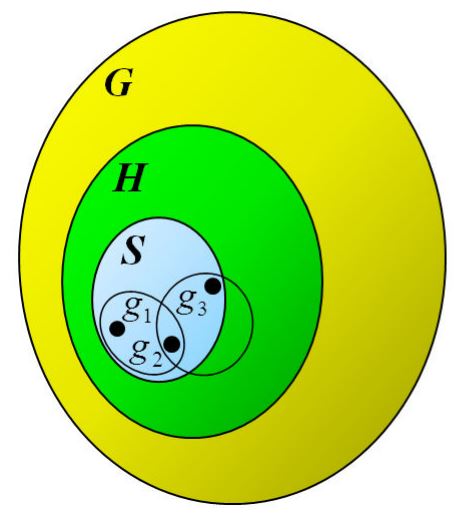
The notion of a sum-free set can be generalised to any group, but we now talk about product-free sets because the notation is multiplicative. If G is a group, and the operation is *, then a subset S of G is product-free when a * b is not in S, for all a, b in S.
In the group of symmetries of the cube, for example, the set of reflections is product-free because the product of two reflections is a rotation. We can ask all the same questions. What is the biggest possible size of a product-free set? Or the smallest locally maximal product-free set? How can we partition the group into product-free sets?
My research – filled groups
I first started looking at these ideas ten years ago, in [1], but have returned to the subject recently with my PhD student Chimere Anabanti [2] – in particular we have been trying to find out more about small locally maximal product free sets. Along the way we have been able to answer a question [2] that has been open since the 1970s about so-called “filled groups” – ones whose locally maximal product free sets have a particular form.
Next steps – Solution-free sets
There is another generalisation of all this, and that is the direction I hope to move in next: we can think of product-free sets as sets having no solution to the equation a * b = c. So we can pick another equation and look for sets that don’t satisfy that equation. The general term for these types of sets is “solution-free sets”.

Professor Sarah Hart
We can ask the same kinds of questions about them as for product-free sets. Examples include Sidon sets – the definition for the integers is a set where all differences are distinct; in other words there are no solutions to a – b = c – d when at least three of a, b, c and d are different.
It’s fun to ponder these ideas in their own right of course, but there are surprising and interesting links to other areas of mathematics. Product-free sets in certain groups give rise to a particularly nice type of error-correcting code. There are also applications to graph theory and to finite geometry. Sidon sets are used in research about the efficient design of sensor arrays.
Find out more
[1] Giudici and Hart “Small maximal sum-free sets”
[2] Anabanti and Hart “Locally maximal product-free sets of size 3” Preprint 10 on this page
[3] Anabanti and Hart “On a conjecture of Street and Whitehead on Locally maximal product-free sets”
Glossary:
- Integer: A whole number (not a fractional number) that can be positive, negative, or zero e.g. -5, 1, 5, 8, 97, 3,043
- Rotational symmetry: When an image is rotated (around a central point) so that it appears two or more times.
- Maximal: A maximal element of a subset S of some partially ordered set (poset) is an element of S that is not smaller than any other element in S